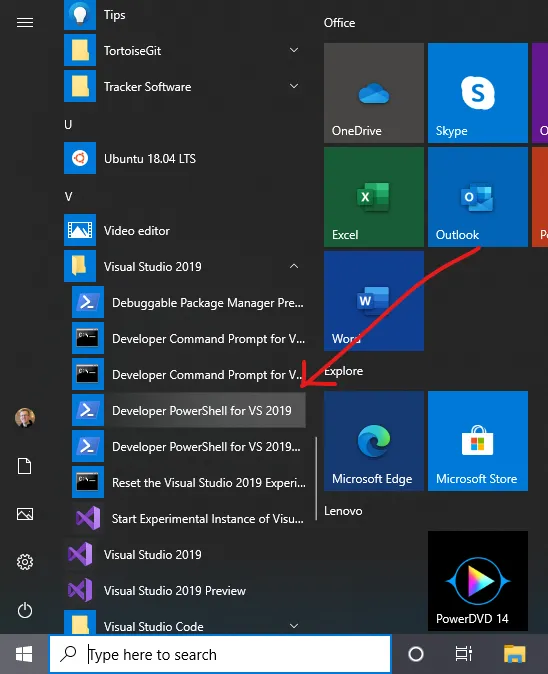
One of the nice new features introduced in Visual Studio 2019 16.2 was the Developer PowerShell for VS 2019 - a nice accompaniment to the existing cmd.exe based Developer Command Prompt for VS 2019.

Windows Start Menu showing Developer PowerShell.

I use PowerShell as much as possible, and for a long time now I've made a habit of updating my profile.ps1 so that all the Visual Studio tools are available from the PowerShell command prompt. Previously this required running the old VsDevCmd.bat batch file and capturing the environment variables it set to then bring them into the PowerShell process. You can see an example here.

But now there's first class support for integrating Visual Studio tooling into your PowerShell environment.

If you take a look at the Windows Start Menu shortcut that's added, you'll see it's defined with a target similar to this:

C:\Windows\SysWOW64\WindowsPowerShell\v1.0\powershell.exe -noe -c "&{Import-Module """C:\Program Files (x86)\Microsoft Visual Studio\2019\Enterprise\Common7\Tools\Microsoft.VisualStudio.DevShell.dll"""; Enter-VsDevShell f9f5056f}"

With the release of PowerShell Core 6, and now PowerShell 7, I'm now favouring these latest releases of PowerShell over the 'legacy' Windows PowerShell 5.1. The problem was until recently, the assembly you see referenced in the shortcut above only worked in Windows PowerShell. It wasn't compatible with PowerShell Core. Pleasingly this was fixed in Visual Studio 2019 16.5.

So now in your PowerShell 7 profile, you can add:

Import-Module "C:\Program Files (x86)\Microsoft Visual Studio\2019\Enterprise\Common7\Tools\Microsoft.VisualStudio.DevShell.dll"
Enter-VsDevShell -InstanceId 9034d7ab

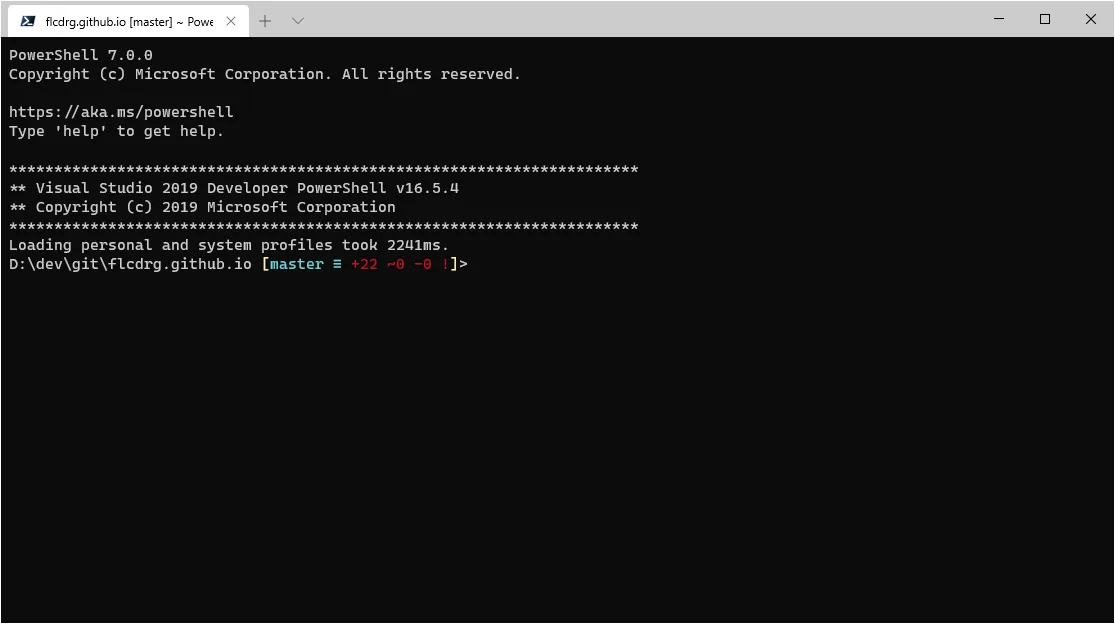
And you'll get the full DevShell experience: !Windows Terminal with PowerShell 7 and Visual Studio integration

There's just one catch - notice that InstanceId? That's unique for every machine. You can either grab the value out of the properties of the Start Menu shortcut, or run vswhere -property instanceId which will return the instanceId of the newest instance of Visual Studio.